14.3、Robot kinematics analysis theory

14.3.1、Precondition

This section will analyze the kinematics equation of four-wheel drive vehicle from the aspect of four-wheel drive vehicle kinematics. Due to the structural error of the real vehicle, there will be resistance, friction and other factors in the process of movement, which is more complex. For simplicity, the analysis is only limited to the four-wheel drive vehicle in the ideal state.

14.3.2、Establish kinematic model

The 4WD car is abstracted into the following model, where W represents the distance between the left and right motor center points; L represents the interval between the front and rear motor center points; Motors M1, M2, M3 and M4 refer to the four driving motors of the trolley; V represents the linear speed of the trolley (forward and backward speed), ω Indicates the angular speed (rotation speed) of the car.

Ideally, by controlling the linear velocity V and angular velocity ω， It is converted to control four motors to control the movement of the 4WD car.

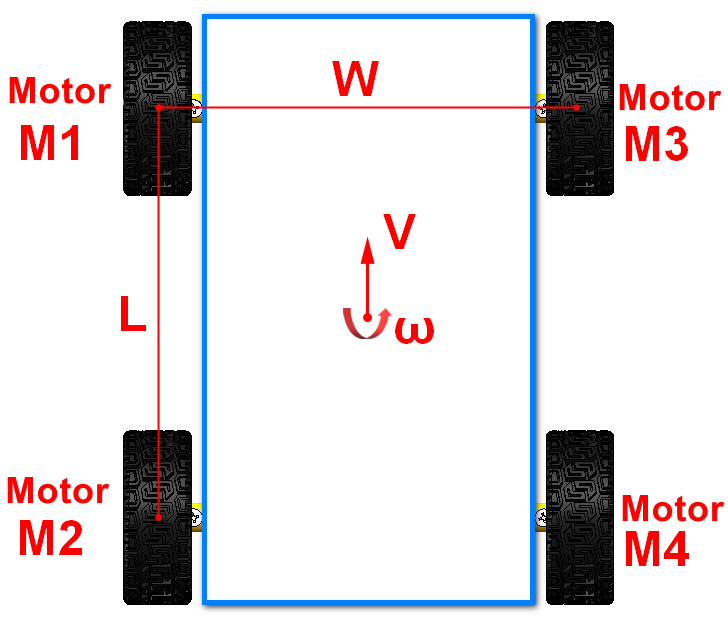
14.3.3、Kinematic analysis

Let V~m1~, V~m2~, V~m3~, V~m4~be the speed values of motors M1, M2, M3 and M4, that is, the rotational speed of wheels, V~x~be the linear speed of the car, V~x~be positive for forward, V~x~be negative for backward, V~z~be the angular speed of the car, V~be positive for left, V~be negative for right, A is half of the distance W between the center points of the left and right motors of the car, A=$ frac {W} {2} $, B is half of the distance L between the center points of the front and rear motors of the car, B=$ frac {L} {2} $.

When the car moves forward or backward.

V~m1~=V~x~

V~m2~=V~x~

V~m3~=V~x~

V~m4~=V~x~

When the trolley rotates around the geometric center point.

V~m1~=-V~z~*(A+B)

V~m2~=-V~z~*(A+B)

V~m3~=V~z~*(A+B)

V~m4~=V~z~*(A+B)

According to the above formula, we can get.

V~m1~=V~x~-V~z~*(A+B)

V~m2~=V~x~-V~z~*(A+B)

V~m3~=V~x~+V~z~*(A+B)

V~m4~=V~x~+V~z~*(A+B)