11.Picture rotation

Image rotation refers to the process of rotating an image at a certain angle according to a certain position. The image still maintains its original size during rotation. After the image is rotated, the horizontal symmetry axis, vertical symmetry axis and center coordinate origin of the image may be transformed, so the coordinates in the image rotation need to be converted accordingly. As shown below:

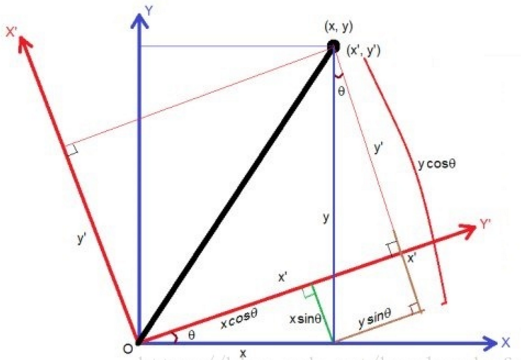
Assuming that the image is rotated counterclockwise by θ, the rotation transformation can be obtained according to the coordinate transformation as：

but

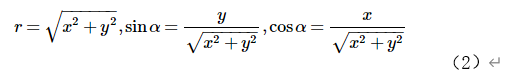
（2）By bringing in (1), we can get:

That is as follows:

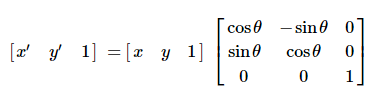
The grayscale value of the rotated picture is equal to the grayscale value of the corresponding position in the original picture as follows:

f(x′,y′)=f(x,y)

The above is the principle of rotation, but the API provided by OpenCV can directly obtain the transformation matrix through functions. The syntax format of this function is:

matRotate = cv2.getRotationMatrix2D(center, angle, scale)

center：center point of rotation

angle：The angle of rotation. Positive numbers are counterclockwise; negative numbers are clockwise.

scale：Transform the scale (zoom the size). 1 means no change, less than 1 means shrinking, and greater than 1 means enlarging.

Code path：/home/yahboom/Dofbot/4.opencv/02_OpenCV Transform/06 pictures rotating.ipynb

import cv2
import   numpy as np
img =   cv2.imread(yahboom.jpg',1)
#cv2.imshow('src',img)
imgInfo =   img.shape
height = imgInfo[0]
width =   imgInfo[1]
matRotate =   cv2.getRotationMatrix2D((height*0.5, width*0.5), 45, 1)# mat rotate 1 center   2 angle 3 scale
#100*100 25  
dst =   cv2.warpAffine(img, matRotate, (height,width))

The following will display the comparison between the original image and the rotated image in the jupyterLab control.

xxxxxxxxxx
#bgr8 to jpeg format
import enum
import cv2
def   bgr8_to_jpeg(value, quality=75):
    return bytes(cv2.imencode('.jpg',   value)[1])

​x
import   ipywidgets.widgets as widgets
image_widget1   = widgets.Image(format='jpg', )
image_widget2   = widgets.Image(format='jpg', )
# create a   horizontal box container to place the image widget next to eachother
image_container   = widgets.HBox([image_widget1, image_widget2])

# display   the container in this cell's output
display(image_container)
#display(image_widget2)
img1 =   cv2.imread('image0.jpg',1)
image_widget1.value   = bgr8_to_jpeg(img1)

    image_widget2.value = bgr8_to_jpeg(dst)