2、Augmented Reality

2.1、Overview

Augmented Reality ("AR"), is a technology that ingeniously integrates virtual information with the real world. It extensively uses a variety of technical means such as multimedia, 3D modeling, real-time tracking and registration, intelligent interaction, sensing, etc., to simulate and apply computer-generated text, images, 3D models, music, video and other virtual information to the real world. In order to achieve the "enhancement" of the real world.

The AR system has three outstanding features: ①The information integration of the real world and the virtual world; ②It has real-time interactivity; ③It adds and locates virtual objects in the 3D space.

2.2、Application

When using the AR case, you must have the camera's internal reference, otherwise it will not work.

2.2.1、Start up launch

Method 1

# USBCam
roslaunch transbot_visual transbot_AR.launch launchCtrl:=True camDevice:=USBCam
# Astra      
roslaunch transbot_visual transbot_AR.launch launchCtrl:=True camDevice:=Astra 

Method 2

xxxxxxxxxx
# USBCam
roslaunch transbot_visual transbot_AR.launch launchCtrl:=False camDevice:=USBCam   
# Astra
roslaunch transbot_visual transbot_AR.launch launchCtrl:=False camDevice:=Astra  

This method can only be started in the successive main controllers that have been connected.

• launchCtrl parameter: If you start usb_cam-test.launch, then this parameter must be set to True.
• camDevice parameters: Obi medium light camera parameters are Astra; high frame rate cameras are USBCam.

Set the parameters according to your needs, and you can also modify the launch file directly, you don't need to attach parameters when you start up.

2.2.2、Effect demonstration

A total of 12 effects.

xxxxxxxxxx
["Triangle", "Rectangle", "Parallelogram","WindMill","TableTennisTable", "Ball", "Arrow", "Knife", "Desk",
"Bench", "Stickman", "ParallelBars"]

Press【F】key to switch between different effects.

You can also switch effects through the command.

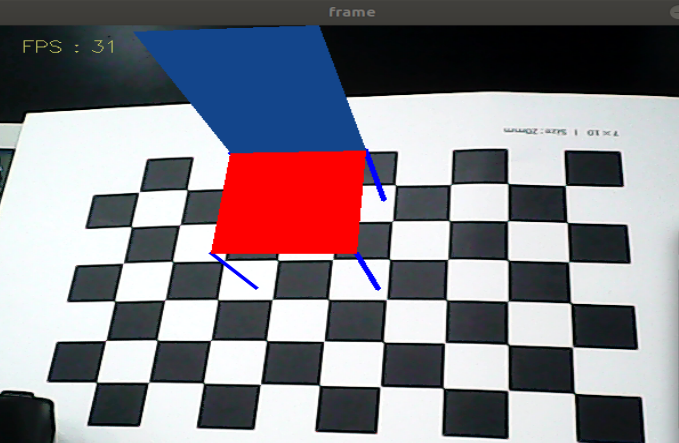
2.3、Code

2.3.1、Algorithm principle

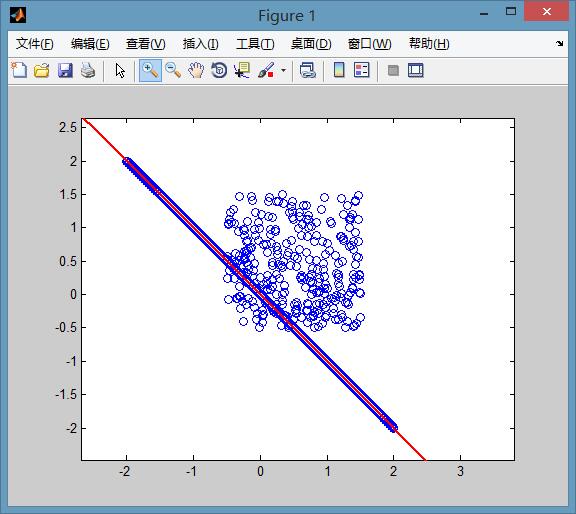
Use the RANSAC scheme to find the object pose from the 3D-2D point correspondence.

The RanSaC algorithm is a classic algorithm for data processing. Its function is to extract specific components in an object under a large amount of noise. The following figure illustrates the effect of RanSaC algorithm. Some points in the figure obviously satisfy a certain straight line, and another group of points is pure noise. The purpose is to find a straight line equation in the presence of a lot of noise, at this time the amount of noise data is 3 times that of a straight line.

2.3.2、Code

launch file

xxxxxxxxxx
<launch>
    <arg name="camDevice" default="USBCam" doc="camDevice type [Astra,USBCam]"/>
    <arg name="launchCtrl" default="fasle"/>
    <arg name="flip" default="false"/>
    <arg name="cam_image_topic" default="/usb_cam/image_raw/compressed"/>
    <node name="simple_AR" pkg="transbot_visual" type="simple_AR.py" output="screen">
        <param name="flip" type="string" value="$(arg flip)"/>
        <param name="launchCtrl" type="string" value="$(arg launchCtrl)"/>
        <param name="camDevice" type="string" value="$(arg camDevice)"/>
        <param name="camera_image" type="string" value="$(arg cam_image_topic)"/>
    </node>
</launch>

python main function

xxxxxxxxxx
    def process(self, img):
        if self.flip == 'True': img = cv.flip(img, 1)
        gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
        # Find the corner points of each picture
        retval, corners = cv.findChessboardCorners(
            gray, self.patternSize, None,
            flags=cv.CALIB_CB_ADAPTIVE_THRESH + cv.CALIB_CB_NORMALIZE_IMAGE + cv.CALIB_CB_FAST_CHECK)
        #Find corner sub-pixels
        if retval:
            corners = cv.cornerSubPix(
                gray, corners, (11, 11), (-1, -1),
                (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001))
            # Calculate object pose solvePnPRansac
            retval, rvec, tvec, inliers = cv.solvePnPRansac(
                self.objectPoints, corners, self.cameraMatrix, self.distCoeffs)
            # Output image points and Jacobian matrix
            image_Points, jacobian = cv.projectPoints(
                self.__axis, rvec, tvec, self.cameraMatrix, self.distCoeffs, )
            # Draw image
            img = self.draw(img, corners, image_Points)
        return img

More function:

https://docs.opencv.org/3.0-alpha/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html

• findChessboardCorners()

xxxxxxxxxx
def findChessboardCorners(image, patternSize, corners=None, flags=None): 
    '''
    Find the corner points of each picture
    :param image: Enter the original checkerboard image. The image must be an 8-bit grayscale image or color image.
    :param patternSize: (w,h)，The number of inner corners in each row and column on the chessboard. w=the number of black and white blocks on a row of the chessboard -1, h=the number of black and white blocks on a column of the chessboard -1.
    For example: 10x6 chessboard, then (w,h)=(9,5)
    :param corners: array，The output array of the detected corner points.
    :param flags: int,Different operation flags can be 0 or a combination of the following values:
    CALIB_CB_ADAPTIVE_THRESH Use the adaptive threshold method to convert the image to black and white instead of using a fixed threshold.
    CALIB_CB_NORMALIZE_IMAGE Before using fixed threshold or adaptive threshold to binarize the image, use histogram to equalize the image.
    CALIB_CB_FILTER_QUADS Use additional criteria (such as contour area, perimeter, square shape) to filter out the false quadrilaterals extracted in the contour retrieval stage.
    CALIB_CB_FAST_CHECK Run a quick check mechanism on the image to find the corners of the board, and return a quick reminder if no corners are found.
    When the chessboard is not observed, the call under degraded conditions can be greatly accelerated.
    :return: retval, corners
    '''
    pass

• cornerSubPix()

We need to use cornerSubPix() to perform further optimization calculations on the detected corners, so that the accuracy of the corners can reach the sub-pixel level.

xxxxxxxxxx
def cornerSubPix(image, corners, winSize, zeroZone, criteria):
    '''
    Sub-pixel corner detection function
    :param image: Input image
    :param corners: Pixel corners (both as input and output)
    :param winSize: The area size is NXN; N=(winSize*2+1)
    :param zeroZone: Similar to winSize, but always has a smaller range, Size(-1,-1) means ignore
    :param criteria: Stop optimization criteria
    :return: Sub-pixel corner
    '''
    pass

• solvePnPRansac()

xxxxxxxxxx
def solvePnPRansac(objectPoints, imagePoints, cameraMatrix, distCoeffs, 
                   rvec=None, tvec=None, useExtrinsicGuess=None, iterationsCount=None, 
                   reprojectionError=None, confidence=None, inliers=None, flags=None):
    '''
    Calculate object pose
    :param objectPoints: Object point list
    :param imagePoints:  Corner list
    :param cameraMatrix: Camera matrix
    :param distCoeffs:   Distortion coefficient
    :param rvec:
    :param tvec:
    :param useExtrinsicGuess:
    :param iterationsCount:
    :param reprojectionError:
    :param confidence:
    :param inliers:
    :param flags:
    :return: retval, rvec, tvec, inliers
    '''
    pass

The RANSAC scheme is used to find the object pose from the 3D-2D point correspondence. This function estimates the pose of the object given a set of object points, their corresponding image projections, camera matrix and distortion coefficients. This function finds a pose that minimizes the re-projection error, that is, the re-observation error, that is, the sum of the squared distances between the observed pixel point projection imagePoints and the object projection (projectPoints()) objectPoints. The use of RANSAC can avoid the influence of outliers on the results.

• projectPoints()

xxxxxxxxxx
def projectPoints(objectPoints, rvec, tvec, cameraMatrix, distCoeffs, imagePoints=None, jacobian=None, aspectRatio=None): 
    '''
    Output image points and Jacobian matrix
    :param objectPoints: 
    :param rvec:   Rotation vector
    :param tvec:   Translation vector
    :param cameraMatrix:  Camera matrix
    :param distCoeffs:    Distortion coefficient
    :param imagePoints: 
    :param jacobian: 
    :param aspectRatio: 
    :return: imagePoints, jacobian
    '''
    pass